On appelle B l’ensemble constitué de deux éléments appelés valeurs de vérité {VRAI, FAUX}, B = {1, 0}, sur cet ensemble on peut définir deux lois (ou opérations), les lois ET, OU et une transformation appelée le complémentaire, l’inversion ou le contraire.
Lois de composition :
Les lois de composition sont des règles logiques qui permettent de simplifier l’écriture des expressions algébriques :
La loi ET, dite conjonction est définie de la manière suivante : a ET b est VRAI si et seulement si a est VRAI et b est VRAI. Cette loi est aussi notée « . »
La loi OU, dite disjonction : a OU b est VRAI si et seulement si a est VRAI ou b est VRAI. Aussi notée 
Le contraire, dit négation : Le contraire de a est VRAI si et seulement si a est FAUX. Egalement notée 
Tables de vérité :
Table de la loi ET |
||
b/a |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
Table de la loi Ou |
||
b/a |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
Propriétés :
Associativité : Comme avec les opérations habituelles en mathématiques, certaines parenthèses sont inutiles : (a + b) + c = a + (b + c) = a + b + c
(a . b).c = a .(b.c) = a.b.c
Commutativité : L’ordre est sans importance : a + b = b + a
a.b = b.a
Distributivité : Comme avec les opérations habituelles, il est possible de distribuer : a.(b + c) = a.b + a.c
Cependant il y a un comportement différent par rapport aux opérateurs + et * habituels : a + (b.c) = (a + b).(a + c)
Idempotence : a + a + a + […] = a et a.a.a.a.[…] = a
Complémentarité : 
Priorité : Ces opérations sont soumises aux mêmes règles que les opérations « normales », la fonction ET (multiplication logique) est prioritaire par rapport à la fonction OU (somme logique), on peut, pour s’aider, placer des parenthèses dans les opérations.
Théorème de De Morgan : 
dans les deux cas, l’expression ne sera VRAIE que si a et b sont fausses.
Dans les deux cas, l’expression ne sera VRAIE que si a ou b sont fausses.
Table de vérité de la somme |
||
a |
b |
a |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
Fonctions logiques fondamentales :
Elles sont issues des trois opérations de base et définissent alors : une fonction de B dans B : le complémentaire ou l’inversion et deux fonctions de B² dans B qui sont la somme (ou OU) et le produit (ou ET)
Table de vérité du produit |
||
a |
b |
a |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
Table de vérité de l’inverse |
|
a |
|
0 |
1 |
1 |
0 |
OU exclusif, dis disjonction exclusive : le OU étudié jusqu’à présent se comprend de la manière suivante : « l’un ou l’autre ou les deux ». Il est également appelé « OU inclusif ». Le OU exclusif (ou XOR) se comprend comme « l’un ou l’autre mais pas les deux ».
Table de vérité de XOR |
||
a |
b |
a |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
Equivalence :
L’équivalence (notée EQV) est vraie si les deux entrées ont la même valeur et fausse sinon.
On peut aussi dire que :
Table de vérité de EQV |
||
a |
b |
aEQVb |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
Implication :
L’implication (notée IMP) s’écrit de la manière suivante :
Cette opération n’est pas commutative. a est une condition suffisante pour b, qui, elle, est une condition nécessaire pour a.
Table de vérité de IMP |
||
a |
b |
a IMP b |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
Inhibition :
L’inhibition (notée INH) se compose de cette façon :
Cette opération n’est pas commutative.
Table de vérité de INH |
||
a |
b |
|
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
Eléments neutres : a + 0 = a et a . 1 = a
Tableau de Karnaugh :
Un tableau de Karnaugh est un tableau de vérité dans lequel les différentes possibilités des entrées sont classées en code GRAY (binaire réfléchi). Ceci correspond à 0 puis 1 dans le cas d’une variable, 00, 01, 11, 10 pour deux variables. On simplifie l’équation d’une fonction en faisant des regroupements sous forme d’une, deux ou quatre lignes ou colonnes. Le tableau de Karnaugh est un tableau étudié pour pouvoir trouver la plus simple équation d’une table de vérité.
Les portes logiques sont les circuits combinatoires les plus simples.
La représentation conventionnelle des portes logiques est la suivante :
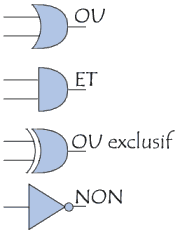
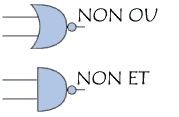
On appelle circuit logique un ensemble de portes logiques reliées entre elles pour répondre à une expression algébrique. Il faut donc transcrire en schéma électrique (à l’aide des représentations ci-dessus) l’expression algébrique que l’on a simplifiée grâce aux lois de composition.
b
b
b